计算机图形学笔记——透视矩阵推导
Posted on 周五 22 十一月 2019 in 计算机图形学
透视矩阵推导
[TOC]
如图:
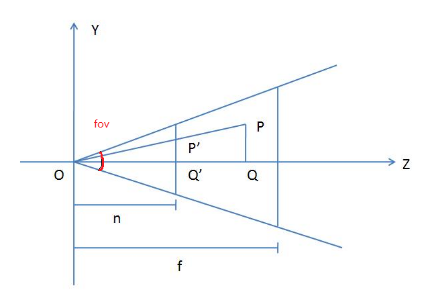
\(O\)点为摄像机所在位置,\(n\)为近剪裁面的距离,\(f\)为远建材面的距离,\(P\)为视锥体中的一个点,\(P'\)为\(P\)在近建材面的一个投影。透视投影矩阵要把位于视锥体内的物体的顶点\(x,y,z\)坐标缩放到\([-1,1]\)范围。这就相当于把这个四棱台扭曲变形成一个立方体。
我们要推导的就是\(P'\)缩放后的坐标\(P''\)。
设\(P(x, y, z), P'(x', y', z'), fov=2\theta\), 可推导:
$$
\frac{x}{x'} =\frac{z}{n} \quad \Rightarrow \quad x'= \frac{nx}{z}
$$
同理:
$$
y' = \frac{ny}{z} \\
z' = n
$$
设\(P\rightarrow P'\) 的变换矩阵为\(M\), \(P'\rightarrow P''\)的变换矩阵为\(N\), 有:
$$
M\cdot \begin{bmatrix}x\\y\\z\\1\end{bmatrix} = \begin{bmatrix}x'\\y'\\z'\\1\end{bmatrix} \quad \quad \quad
N\cdot \begin{bmatrix}x'\\y'\\z'\\1\end{bmatrix} = \begin{bmatrix}x''\\y''\\z''\\1\end{bmatrix}
$$